平均と標準偏差を使って
身長が大きいか小さいか
おおざっぱに判断をすることができます。
平均 ー3×標準偏差 結構小さい
平均 ー2×標準偏差 小さい
平均 ー1×標準偏差 普通の中では小さい
平均 普通
平均 +1×標準偏差 普通の中では大きい
平均 +2×標準偏差 大きい
平均 +3×標準偏差 結構大きい
↑の意味が分からない人は過去記事をみてください。
過去記事
平均と標準偏差 その1:大雑把に大きいか小さいかが分かる
身長の大きさって、小さい順に並んだとき前から何番目にいるのか、
ということで判断できますよね。
身長の順番を求めることができることです。
ここでは、 パーセンタイル値を使って順番を求める方法を説明します。
パーセンタイル値とは:
データを小さい順に並べて、前から数えて〇〇パーセントの場所にある値を〇〇パーセンタイル値と呼びます。〇〇には0から100の間の数が入ります。
詳しくは過去記事 をみてください。
正規分布のパーセンタイル値について簡単に説明します。
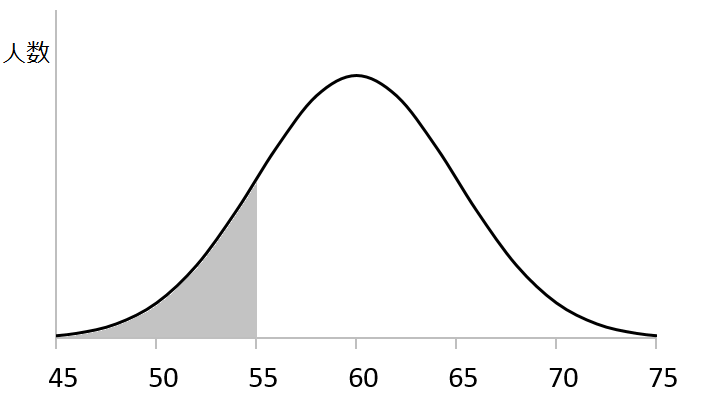
下のグラフをみてください。
グラフの縦軸を人数と思ってもいいのですが、
「面積が人数」と思う方が理解しやすいでしょう。
平均体重60kgの人たちのグラフだと思えばイメージしやすいかもしれません。
灰色に塗られた部分に注目してください。
小さい順で並んだとき55kg より軽い人たちが灰色の部分にいます。
正規分布の場合、灰色の面積はどのくらいの大きさか計算することができます。
今回の例では、山全体の面積を100%としたとき、
灰色の部分の面積は15.9%になります。
小さい順に並んだとき前から15.9%のところに55kgの人がいる、ということです。
この結果から、
15.9パーセンタイル値は55kg
となります。
15.9という数自体にそれほど意味はありません。
灰色部分の面積を数学的に計算すると全体の15.9%になった、
というだけです。
灰色部分の面積の計算方法は覚える必要はありません。
ここで重要な点は、
正規分布の場合、パーセンタイル値を求めることができる
ということです。
ただし、平均と標準偏差の値が分かっていないと
パーセンタイル値を求めることはできません。
パーセンタイル値が幾つになるのかは、
次の表のようにまとめられます。
|
〇% |
〇パーセンタイル値 |
|
0.1% |
平均 ー3×標準偏差 |
|
2.3% |
平均 ー2×標準偏差 |
|
15.9% |
平均 ー1×標準偏差 |
|
50.0% |
平均 |
|
84.1% |
平均 +1×標準偏差 |
|
97.7% |
平均 +2×標準偏差 |
|
99.9% |
平均 +3×標準偏差 |
注) この表は正規分布するときのみ正しいです。
表中の細かい数字の意味は気にしなくてよいです。
この表の使い方を覚えたほうが良いです。
この表の使い方を具体例を使って説明したいと思います。
「身長は正規分布する」と統計の世界で扱われることが多いので、
身長を例に説明します。
例えば、
2015年度の女児の身長の平均値と標準偏差は下表のとおりです。

例えば、女子、幼稚園(5歳)の場合、
平均は 109.4 cm
標準偏差は 4.66 cm
ですので
109.4 - 3×4.66 = 95.42 cm
より身長が低い人は全体の 0.1%
109.4 - 2×4.66 = 100.08 cm
より身長が低い人は全体の 2.3%
109.4 - 1×4.66 = 104.74 cm
より身長が低い人は全体の 15.9%
109.4 cm
より身長が低い人は全体の 50.0%
109.4 + 1×4.66 = 114.06 cm
より身長が低い人は全体の 84.1%
109.4 + 2×4.66 = 118.72 cm
より身長が低い人は全体の 97.7%
109.4 + 3×4.66 = 123.38 cm
より身長が低い人は全体の 99.9%
と判断すると良いです。
表にまとめるとこうなります。
|
〇% |
身長 |
|
0.1% |
95.42 cm |
|
2.3% |
100.08 cm |
|
15.9% |
104.74 cm |
|
50.0% |
109.4 cm |
|
84.1% |
114.06 cm |
|
97.7% |
118.72 cm |
|
99.9% |
123.38 cm |
例えば、自分の子が5歳の女児で 115 cmだったとします。
このときは、
上の表を見ると114.06 cmよりも低い人が全体の84.1%だから、
100人が小さい順にならんだとき、
前から84番目が約114 cmってことだよなぁ・・・
ん!?
ってことは、自分の子は115cmだから
84番目よりちょっと後ろにいるってことか~!
って感じになります。
ところで、115 cmの子が前から何番目にいるのかを、
もっと正確に求めることもできます。
その方法に興味がある方は過去記事をご覧ください。
過去記事
今回はここまでにしたいと思います。
質問・疑問等がありましたら、お気軽にコメントしてください。