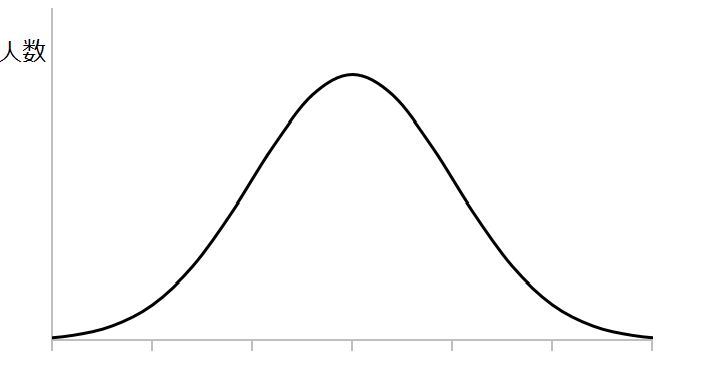
正規分布とは、こんな形のグラフです。
横軸が測定値、縦軸が人数と思って下さい。
この正規分布の山の形は、
数学的に厳密に決まっています。
山の曲がり具合とかも、
数学的に正確に決まっているのです。
ここで理解しておいた方が良いポイントとしては、
数学の理論として正規分布という形のグラフがある、ということです。
理論上のグラフだから、綺麗な形をしています。
一方、現実に何かを測定してグラフを作成したときは
グラフの形は正規分布と比べて凸凹とした形になるでしょう。
しかし、凸凹してるけど、なんだか正規分布っぽい形をしている、
ってことがあるんです。
そういうとき、多少の誤差はあるけど、似たような形だから
正規分布してるとみなしてしまうことがあります。
多少の誤差は気にしない、ってことです。
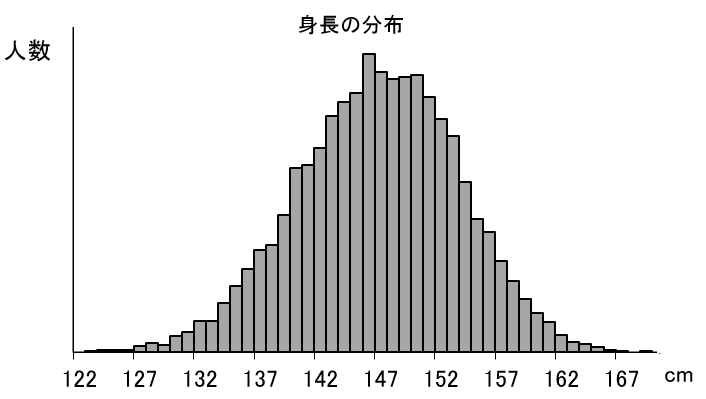
例えば、同年代同性の身長のグラフはこんな感じです。
正規分布っぽいですよね。
だから、身長のグラフは正規分布の形をしている、って考えていいです。
これを「身長は正規分布に従う」って言ったりもします。
分布に従う、って言い方はなんだか不思議な表現ですが、
まあ、専門用語だと思ってください。
正規分布は数学の話ですので、数学的にいろいろと計算して、
様々なことが分かっています。
数学の理論上、正規分布する、ということが分かっているものもあります。
あくまでも理論上ですので、現実に何かを測定してグラフを作成する、
という話ではありません。
数学の理論としての正規分布が何の役にたつのかといいますと、
と予想できるようになるということです。