正規分布って統計とかで出てくるけど、
これが出てきたら、思い出すべき用語があります。
それは、
平均と標準偏差
です。
標準偏差とは何?って思う人は過去記事を見てください。
これがない、ってことはあり得ません。
それくらい、
平均と標準偏差
は大事なものです。
次に、思い浮かべて欲しいのは、
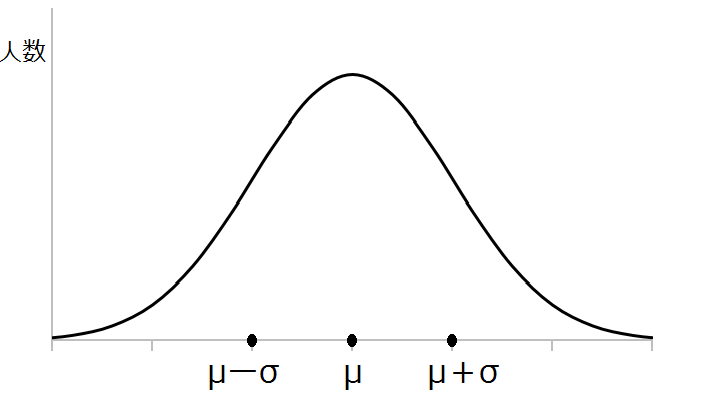
山の頂上が真ん中にあり、左右対称になだらかに減っていくグラフ。
この形のグラフを正規分布と呼びます。
さて、このグラフに2つの記号が書いてありますね。
μ はミュー
σ はシグマ
と呼びます。これは平均と標準偏差のことです。
平均、標準偏差とグラフの中に書くのは難しいので
μ = 平均
σ = 標準偏差
と短い表現に書き直した、と思ってください。
具体例で説明したほうが分かりやすいと思いますので、
今回は身長を身体測定した、という話に例えて説明します。
同学年で同性の人達の身長を測定した結果を
横軸が身長、縦軸が人数のグラフで表すとします。
このグラフが
という形をしているとします。
μ は平均身長。 σ は身長の標準偏差です。
高学年になるほど平均身長が大きいですよね。この場合、μ が大きくなります。
標準偏差とはバラツキの大きさと思ってください。
「標準偏差 」という単語を「バラツキ」と読み替えてみましょう。
標準偏差が小さいとき、身長のバラツキが小さい。
標準偏差が大きいとき、身長のバラツキが大きい。
同じような身長の人ばかりのグラフを描くときは、σは小さいです。
身長差がある人達のグラフのときは、σ は大きくなります。
このように、 μ と σ の値に応じて身長のグラフを描くことになります。
例えば
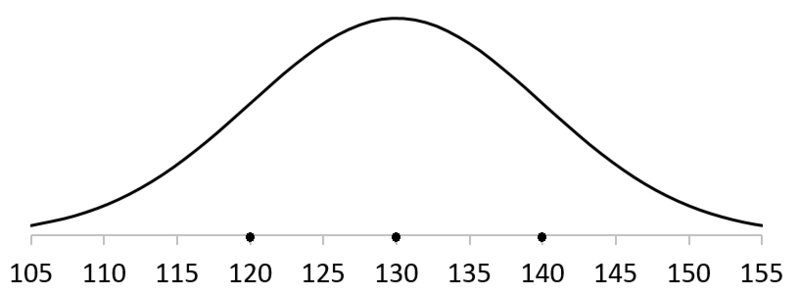
μ=130cm、σ=10cm
のときは
μーσ=120、μ+σ=140 ですので、次のようになります。
μ=130cm、σ=5㎝
のときは
μーσ=125、μ+σ=135 ですので、
σが小さいとき、身長のバラツキが小さいので、
多くの人が平均130cmと似たような身長です。
130cm 付近に大勢の人がいることを表したいときは、
細くて高い山を描くと良いでしょう。
重要なのは次のことです。
-
μとσの値が決まれば、具体的に1つの身長のグラフを描くことができる。
今回の話は
正規分布≒身長のグラフ
で例えて解説しました。
まとめ
-
μとσの値が決まれば、具体的に1つの正規分布が定まる。
母平均と標本平均
身長を考えるとき、統計では平均は2つあります。
母平均と標本平均です。
母平均は全員の身長を平均したものです。
でも、全員の人数が多すぎて身長を調べられないことがあります。
このとき、全体から少しずつ人を選び出して、
その人たちの身長を平均することがあります。
これを標本平均といいます。
統計では、母平均を μ と書くことが多いです。
今回はここまでにしたいと思います。
質問・疑問等がありましたら、お気軽にコメントしてください。