正規分布って何?
って思うことありますよね。
まあ、難しいこと抜きにして、
正規分布は平均値について考察するときに出てくる用語です。
平均値というのは、いわゆる平均。
例えば、平均点とかそういうのです。
正規分布が何の役に立つのか、
ということは別の記事に書くことにします。
今回は、正規分布とは何か、ということをテストの点を例に説明したいと思います。
横軸を点、縦軸を人数としたグラフを描きたいとします。
では、 平均点を60点だとして、
テストの点のグラフを想像してみてください。
平均60点だからといって、60点の人数が多いとは限りません。
例えば
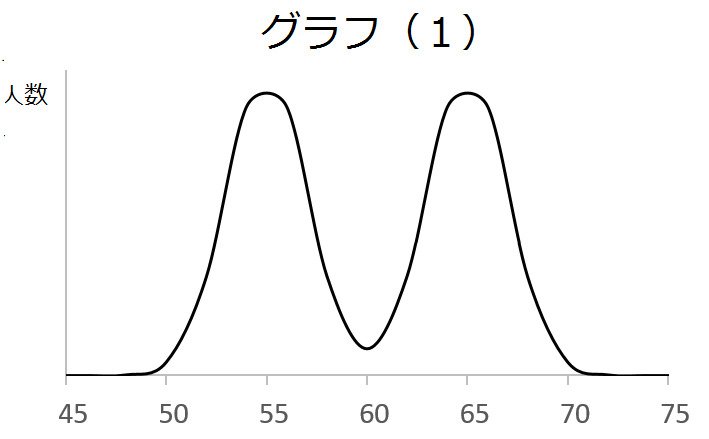
このグラフ、真ん中に60点があるので、
平均60点になっています。
でもなんだか不自然ですね。
何で、平均近くの人がいないの?って気がします。
何か理由があるの?って聞きたくなりますね。
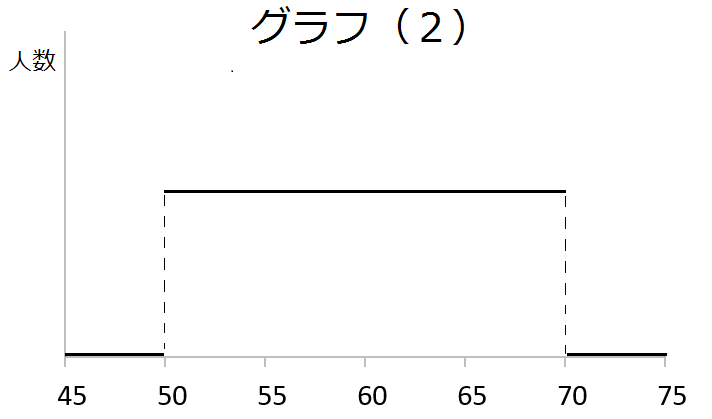
では、こんなのはどうでしょう?
これも平均60点です。
悪くはないけど、50点以下の人が突然いなくなるのは不思議ですね。
70点以上の人も突然いなくなります。
もっと、自然な感じに描いてみましょう。
次のグラフも平均60点です。
さっきよりましだけど、
平均60点の人よりも、
平均より低い56点辺りの人の人数が多いですね。
平均より低い人の方が多い理由は何かあるの?
って聞きたくなります。
では、次のはどうでしょう?
平均点の所に山の頂上があり、左右対称になだらかに減っていくグラフ。
平均60点のテストのグラフというと、
こういうのをイメージする人が多いと思います。
このグラフ(4)を正規分布と呼ぶと思ってください。
まとめ
-
グラフ(4)を正規分布と呼ぶ
この理解で大体OKです。
ここからは、ちょっと補足。
今回の話は、分かりやすくする為に、テストの点の話にしました。
実は、テストの点のグラフは(4)のようになるとは限りません。
(1)(2)(3)のようになることもあり得ます。
テストの点の場合、
0点未満はあり得ないとか、
100点より上の人はいないよねとか、
グラフを描く際に色々な条件が付け加えられます。
このような条件のおかげで、
より正確なグラフが描けるようになります。
例えば、学力が2極分化している場合は、
グラフ(1)のように描いた方が良いでしょう。
このようにテストの点のグラフは、
「平均値以外の条件」も使って描くことがありますので、
必ずしも正規分布になるわけではありません。
正規分布 、t分布、F分布
統計では正規分布以外にも、t分布、F分布といったものが出てきますが、
その基本は正規分布なのです。
だから、正規分布は重要なんです。
今回はここまでにしたいと思います。
質問・疑問等がありましたら、お気軽にコメントしてください。