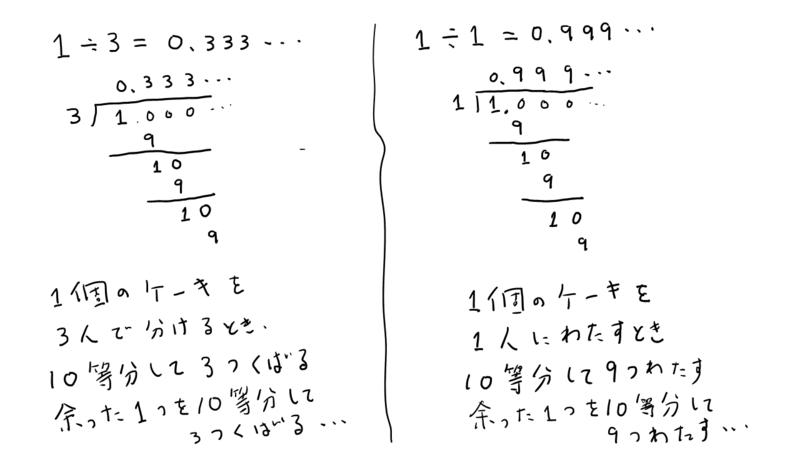くものしゅの日記

子育て中の ph. D.です。専門は確率統計.情報理論等

幼児教育と数学（その１）順序数とペアノの公理

子育て 数学 STEM 雑談 教養 教育
幼児教育では
順序数
集合数
が理解できれば数の概念が身についた、ってことになるそうです。
 
「順序数」は、順序を表す数のこと。
順番のことですね。
これが1番目、これが2番目、これが3番目、…
と順番が分かれば、順序数が理解できていることになります。
 
「集合数」とは、ものの多さを表す数のこと。人数とか個数のことですね。
 
幼児教育では、順序数と集合数の両方が分かったら、数の概念が分かった、となるようですが、数学的にはどうなんでしょう？
 
数とは何か？
数学では、自然数はペアノの公理で定義できます。ペアノの公理とは、
一番最初、その次、その次、・・・
と、順番に数えるという動作を、論理的に記述したものです。
ウィキペディアによるとこんな感じです。
 

ペアノの公理は以下の様に定義される。

自然数は次の5条件を満たす。

  1. 0は自然数である。
  2. 任意の自然数 a にはその後者 (successor)、suc(a) が存在する（suc(a) は a + 1 の "意味"）。
  3. 0 はいかなる自然数の後者でもない（0 より前の自然数は存在しない）。
  4. 異なる自然数は異なる後者を持つ：a ≠ b のとき suc(a) ≠ suc(b) となる。
  5. 0 がある性質を満たし、a がある性質を満たせばその後者 suc(a) もその性質を満たすとき、すべての自然数はその性質を満たす。
 

結構難しいですね…

でも大丈夫！
大雑把にいうと、
順番に数えるという動作を、論理的に記述したら、ペアノの公理になる
ということです。つまり、
数を数えることができるなら、ペアノの公理を（無意識的に）理解していると言えるのです。
つまり、
 
数えることができる
　↓
ペアノの公理が（無意識的に）使える
 
ということ。
 
幼児教育の話に戻りますと
 
順序数が理解できる
　↓
数えることができる
　↓
ペアノの公理が（無意識的に）使える
 
となります。
幼児教育って難しいですね。
 
続く
 

1 = 0.999…の件、その８（位相に着目）

数学 教養 雑談 教育
1=0.999…　（9は無限に並ぶ）
って本当？
1>0.999…
でしょ？
 
という質問に対する答えは難しい。

0.999... - Wikipedia

によると
等式 0.999… = 1 は数学者に長く受け入れられ、一般の算数・数学教育の一部であったにも拘らず、これを十分直観に反するものと見なして、疑念や拒絶反応を示す学徒もいる。このような懐疑論は、「この等式を彼らに納得させることがいかに難しいか」が数学教育の様々な研究の主題となることに正当性を与える程度に当たり前に存在している。
つまり、
1=0.999…
は納得できなくて当たり前なのです。当然、1=0.999…の証明も納得しづらいです。
まとめると、こんな感じです。
 
1=0.999…が成り立つ話。
実数の場合、1 = 0.999…は成り立ちます。
実数とは、簡単に言うと、普通の数のこと。特に難しく考える必要ありません。1 と 0.999…を同一視するから
 1 = 0.999…
が成り立つ、ということです。
 
1 ≠ 0.999…が成り立つ話。
1 ≠ 0.999…の場合は難しいので、次の2つに分けて考えてみます。
  • 1 と 0.999… は近い数だけど異なる。
  • 1 と 0.999… は全く異なる。
 

1 と 0.999… は近い数だけど異なる。
1 と 0.999…は、ほぼ同じだけど、0.999…の方が若干小さい、と直感的に感じる方も多いと思います。これは、近い遠いの基準（位相）が細かくて、小さな違いが見分けられる、ということです。通常よりも小さな違いを見分けられる、ということですので、なんの問題もありません。しかし、大抵の場合は、小さな違いは重要ではないので、1 と 0.999…を同一視して
1 = 0.999…
が成り立つ、とした方がシンプルになります。

 

1 と 0.999… は全く異なる。
1 と 0.999…が、ほぼ同じどころか、全く違う数に感じる、という状況です。これは、近い遠いの基準（位相）が通常と異なっているので、1 と 0.999…が近い数だと思えない、ということです。これは難しいので、一言で言い表せません。ただ、重要なのは、

 

1 と 0.999… が全く異なっても数学的に問題はない、ということです。

 

近い、を、似てる、と言い換えたほうが分かりやすいかもしれません。

整数2、3、128 を例に説明します。
大きさが基準の場合
  • 2と3は似ている。2と128は似ていない
偶数か奇数かが基準の場合
  • 2と128は偶数だから似ている。2と3は偶数と奇数だから似ていない。
このように、数の、どの性質に着目するかで、似てるかどうかは変わります。よって
 
1 と 0.999… は全く似ていない
 
という考え方も数学的にはありなのてす。
 
読んでくれてありがとうございます。

1=0.999…の件、その7　（数列の極限？）

数学 教養 教育 雑談
0.999…を数列
0.9
0.99
0.999
…
の極限と考えれば
1=0.999…
が証明できるという話があります。
 
定理：
1=0.999…
数列の極限とみなす証明：
0.999…を数列と見なす。
0.999…は1に近づくので
0.999…=1
□
 
この証明には、1つ気になる点があります。それは、
 
0.999…は1に近づく
 
のところ。本当に 0.999…は1に近づきますか？
 
この疑問のポイントは、
2つの数が近い
の意味です。普通に考えれば、0.999…は1に近づく、は正しそうです。しかし、「近い」の意味が通常と違う場合はどうでしょう？
 
近いとか遠いという概念は、数学では、位相空間論で定義します。
位相空間って何？　
って人も多いかと思いますが、安心してください。難しい数学は必要ありません。
 
位相とは、近い遠いの基準
 
と思ってください。何が近いか、何が遠いか、その判断基準のことを位相という、と思えば、大体オッケーです。
 
海の生き物、サメ、イルカ、タツノオトシゴを例に説明してみます。
見た目で言うと、サメとイルカは似てますが、サメとタツノオトシゴは似ていません。
もし、近い遠いの基準（位相）が、「見た目」の場合、
サメとイルカは近いが、サメとタツノオトシゴは遠いといえます。
 
ところで、サメとタツノオトシゴは魚類ですが、イルカは哺乳類です。もし、近い遠いの基準（位相）を遺伝子 DNAとすると、
サメ（魚類）とタツノオトシゴ（魚類）は近いが、サメ（魚類）とイルカ（哺乳類）は遠いといえます。
 
見た目という位相
遺伝子 DNAという位相
このように位相が違えば、何が近いか何が遠いかが変わる、ということです。
 
数の場合でも、近い遠いの基準（位相）が違えば、何が近いか何が遠いかが変わるのです。
 
0.999…と1は数の大きさは似ています。もし、近い遠いの基準（位相）を数の大きさとすると、0.999…と1は近いといえます。この場合、0.999…を数列の極限とみなすと
0.999…=1
がいえます。
と言えるでしょう。しかし、近い遠いの基準（位相）が通常と違うならば、0.999…を数列の極限とみなしても
0.999…は1になりません。
 
近い遠いの基準（位相）が通常とは異なる例は
に書いてあります。興味のある方は読んでみてください。
 
続く
 
読んでくれてありがとうございます。
 

1=0.999…の件、その6

数学 教養 教育 雑談
1=0.999…　（9は無限に並ぶ）
って本当？
1>0.999…
でしょ？
 
という質問に対する答えは難しい。

0.999... - Wikipedia

によると
等式 0.999… = 1 は数学者に長く受け入れられ、一般の算数・数学教育の一部であったにも拘らず、これを十分直観に反するものと見なして、疑念や拒絶反応を示す学徒もいる。このような懐疑論は、「この等式を彼らに納得させることがいかに難しいか」が数学教育の様々な研究の主題となることに正当性を与える程度に当たり前に存在している。
つまり、
1=0.999…
は納得できなくて当たり前なのです。当然、1=0.999…の証明も納得しづらいです。
 
 
前回までは、代数的な証明の納得しづらさについて説明しました。今回は、解析的な話。実数で考える、という話をします。
 
1=0.999…
が成り立つのは、実数で考えてるからです。実数というと、分かりづらいです。実数って何者？デデキントの切断とかで定義するんですけど、まあ、分かりづらい。
 
でも、安心してください。実は簡単なんです。
 
1=0.999…
が成り立つ理由は、本当に単純な話なんです。
 
実数で考えると
1=0.999…
で成り立つ理由は、
1と0.999…を同一視してるからなんです。
 
本来は違うものだけど、同一視しているから、イコールが成り立つのです。
1と0.999…を同一視する
ということは、
1－0.999… を 0 と同一視する、
と同じです。本来、
1- 0.999…= 0.000…01
のように、0が無限に並び最後に1が付くので、 0 でないけど、0.000…01 と 0 を同一視すれば
1- 0.999…= 0
が成り立つといえるのです。
 
ようは、本来違うものを同じものであると同一視している、ということなんです。
 
嘘だと思うなら、実数のコーシー列による構成、を調べてみてください。
コーシー列 - Wikipediaにも書いてあります。

有理数 q は、常に一定値 q を値にとる数列 (q, q, q, …) と同一視して、有理数全体の成す集合 Q は、有理コーシー数列全体の集合 X に含まれるものと見なす。また、コーシー列に、項同士の四則演算をもとに四則演算を定義することができ、これは有理数同士の四則演算と両立している。特に、X は (0, 0, 0, …) を零元、(1, 1, 1, …) を単位元とする環である。ここで、(xn) − (ym) が 0 に収束するという関係 ∼ は同値関係になる。この同値関係 ∼ で割った[注 3]商環 X/∼ は、同型の違いを除いて一意的に決まる。この X/∼ を R と書き、実数体とよぶ。

 

・・・読んでみても分からなかった、という人でも大丈夫。大雑把に言うと、こんな話です。
 
～ ってのが同一視する、という意味です。因みに
1～0.999…
が成り立つんですけど、これは
1と0.999…を同一視する
ってことです。んで、
「有理コーシー数列全体の集合 X を～で割った商空間 X/～ を実数体と呼ぶ」みたいな話は
実数では 1と0.999…を同一視するからよろしくね、
ってことです。
 
・・・難しいことは気にしなくてもよいです。
 
重要なのは、ただ一つ。
 
実数では1 と 0.999… を同一視するから、
1=0.999…
が成り立つ、
 
ということです。
 
続く
 
読んでくれてありがとうございます。

1=0.999…の件、その5（−1 = …999 の件）

教養 教育 数学 雑談
1=0.999…　（9は無限に並ぶ）
って本当？
1>0.999…
でしょ？
 
という質問に対する答えは難しい。

0.999... - Wikipedia

によると
等式 0.999… = 1 は数学者に長く受け入れられ、一般の算数・数学教育の一部であったにも拘らず、これを十分直観に反するものと見なして、疑念や拒絶反応を示す学徒もいる。このような懐疑論は、「この等式を彼らに納得させることがいかに難しいか」が数学教育の様々な研究の主題となることに正当性を与える程度に当たり前に存在している。
つまり、
1=0.999…
は納得できなくて当たり前なのです。当然、1=0.999…の証明も納得しづらいです。
 
前回は、位取り記数法を使うと
1=0.999…
と
−1 = …999.
の両方が証明できることを説明しました。
 
−1 = …999.
は、一見不思議ですが、必ずしも間違いとは言えません。
「等比級数の解析接続」という魔法の言葉で
−1 = …999.
を正当化できるし、コンピュータ等でマイナスを扱う際にビット反転する話に似ており、実用性もあります。
 
というわけで
1=0.999…
と
−1 = …999.
の両方とも正しい、としましょう。そうすれば
1-1=0
より
…999.999… = 0
がいえます。9が左右に無限に並んでいるとき0になります。これは9に限りません。
実は
…000.000… 　0が無限に並ぶ
=…111.111… 　1が無限に並ぶ
=…222.222… 　2が無限に並ぶ
=…333.333… 　3が無限に並ぶ
･･･
=…999.999… 　9が無限に並ぶ
= 0
となります。証明はこんな感じ。
 
定理：
…aaa.aaa…=0
証明：
x=…aaa.aaa… 
と置く。
10x=…aaa.aaa… =x
より
x=0
□
 
続く
 
読んでくれてありがとうございます。

1=0.999…の件、その4

数学 教養 教育 雑談
1=0.999…　（9は無限に並ぶ）
って本当？
1>0.999…
でしょ？
 
という質問に対する答えは難しい。

0.999... - Wikipedia

によると
等式 0.999… = 1 は数学者に長く受け入れられ、一般の算数・数学教育の一部であったにも拘らず、これを十分直観に反するものと見なして、疑念や拒絶反応を示す学徒もいる。このような懐疑論は、「この等式を彼らに納得させることがいかに難しいか」が数学教育の様々な研究の主題となることに正当性を与える程度に当たり前に存在している。
つまり、
1=0.999…
は納得できなくて当たり前なのです。当然、1=0.999…の証明も納得しづらいです。
 
今回は、代数的な証明の中の位取り記数法の性質を用いた証明（と、その納得しづらさ）について説明します。
 
定理：
1 = 0.999…
位取り記数法の性質を用いた証明：
x = 0.999…　（1）
の両辺を10倍すると
10x=9.99…　（2）
である。（2）−（1）より
9x=9
両辺9で割ると
x = 1
であるので（1）より
1 = 0.999…
□
 
これは正しそうですが（1）を10倍して（2）が導き出すところが納得しづらいです。10倍すると小数点の位置が
0.999…　
↓10倍
9.99…
とズレるという発想が怪しいのです。因みに、この発想を
0.999…　（9が無限に右に並ぶ）
ではなく
 …999.　（9が無限に左に並ぶ）
に適用するとこんな定理が成り立ちます。
 
定理：
−1 = …999.
位取り記数法の性質を用いた証明：
x = …999.0　（1）
の両辺を10倍すると
10x=…9990.　（2）
である。（2）−（1）より
9x=-9
両辺9で割ると
x = -1
であるので（1）より
−1 = …999.
□
 
 …999.　（9が無限に左に並ぶ）
は無限に大きな数のはずです。−1 = …999 が証明できるって、なんだか怪しい！……という感じで、位取り記数法による証明は納得しづらいのです。
 
実のところ、位取り記数法において
−1 = …999.
であるということは、おかしな話ではないのです。実際、…999に1を足すと、桁が繰り上がっで
 
…999+1 = …000
 
となり、0になります。1を足すと0になる数が−1であることは不自然ではないです。
 
この構造、二つを並べて比べると、分かりやすいです。
 
1-0.999…= 0.00…　右に0が続き最後に1がある？
…999+1 = …000　左に0が続き最後に1がある？
 
0がずーっと続いたあとに1がある、とも言えるし、ないとも言えるし、どっちがいいでしょうか？
 
どちらにせよ、位取り記数法の性質から
1-0.999…= 0.00…=0
と
…999+1 = …000=0
の両方が証明できます。
 
続く
 
読んでくれてありがとうございます。

1=0.999…の件、その３（1÷1 を計算すれば証明できる）

雑談 数学 教養 教育
1=0.999
の証明なんですけど、分数を使った証明は、まだるっこいです。
 
1÷3=0.333…
を3倍して
1=0.999…
 
のように、3で割って3をかける、とか
 
1÷9=0.111…
を9倍して
1=0.999…
 
のように、9で割って9をかける、とか、「同じ数を割ってかける」と、2回も計算しています。
 
そんな遠回しな計算する必要はあるのでしょうか？
 
いきなり
 
1÷1=0.999…
 
でいいと思うのです。これだと割り算1回ですみます。
 
筆算で、ちゃんと計算できます。

 
続く
 
読んでくれてありがとうございます。
 
過去記事