平均と標準偏差その3 で説明したことですが、
エクセルの関数
NORM.DIST(x,平均,標準偏差,TRUE)
を使うとデータ x が何パーセンタイルであるか求めることができます。
ただし、この関数を使ってよいのは正規分布するときです。
正規分布とは何か、ということについては今回は気にしなくても良いです。
今回は、NORM.DIST関数を使ってパーセンタイル値を求めた結果が、本当に正しいかどうか、ということについて考えてみたいと思います。
平均と標準偏差その3の例を使います。
例:
2015年度の学校保健統計調査(文科省)によると
女子、幼稚園(5歳)の身長は以下の通りです。
平均は 109.4 cm
標準偏差は 4.66 cm

自分の子が5歳の女児で 115 cmとします。
Excelのセルに
=NORM.DIST(115, 109.4, 4.66, TRUE)
と入力すると、0.885 と表示されるので、
115 cm は 88.5パーセンタイル値です。
では、この結果が本当に正しいのか確認したいと思います。
学校保健統計調査 平成27年度 参考(学校保健統計調査による身体発育値及び発育曲線)
に実際のパーセンタイル値が書いてあります。
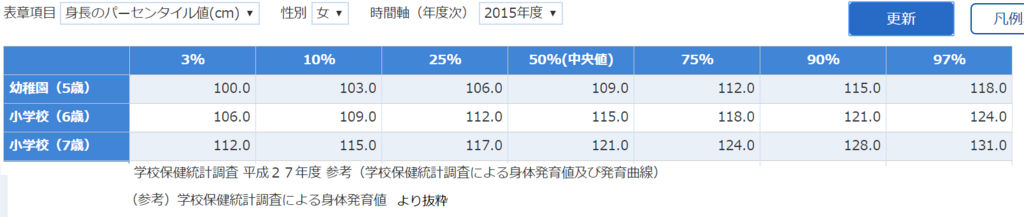
幼稚園(5歳)の90パーセンタイル値は 115 cm です。
つまり、こういうことです。
115 cm は何パーセンタイル値かというと、
88.5 パーセンタイル値(平均と標準偏差を使って求めた値)
90 パーセンタイル値 (実際の値)
だいたい同じですね。
でも、微妙に違う値です。どういうことでしょうか?
実は、平均と標準偏差を使ってパーセンタイル値を求める方法は
誤差が発生します。
88.5 ー 90 = ー 1.5
は誤差と思ってください。
そして、身長がある性質を満たすとき、誤差が0になります。
その性質を「正規分布」といいます。
誤差が0になるとき、正規分布する、
誤差はほぼ0になるとき、ほぼ正規分布する、
誤差が大きな値になるとき、正規分布しない、
と呼ぶことにしましょう。
身長の場合、誤差はあるといえばありますが、
誤差は小さいので、誤差は0に近いとも言えます。
ですので、身長は、ほぼ正規分布する、と考えて良さそうです。
ところで、
赤ちゃんの発育曲線って? その4
って感じです。
多少の誤差が発生することもありますが、
平均身長と標準偏差を使ってパーセンタイル値を求める方法は、
正しいと考えて良いとされています。
まとめ:
-
実際のパーセンタイル値が分かっているならば、それを使う。
「平均と標準偏差」についての解説は今回で一区切りとします。
過去記事はこちら